Factorization Machines(FM) 和 Field-Aware Factorization Machine(FFM)：推薦系統中的瑞士軍刀

發表於 分類於 文章字數： 2.3k
FM速度快、容易實作，於2012~14年為業界主流模型

Factorization Machines(FM)

  • SVM
    • 難以在稀疏資料中學習
  • Factorization Models(如Matrix Factorization)
    • 擴展性低：需要特定的輸入格式

FM：克服SVM和Factorization Models的缺點

  • 可在稀疏資料中學習
  • 輸入資料可擴展
  • 訓練時間為線性複雜度

理論

FM將權重 $w_{ij}$ 設為兩個長度為k的隱向量$V_i, V_j$的內積，表示為$\langle V_i, V_j \rangle$

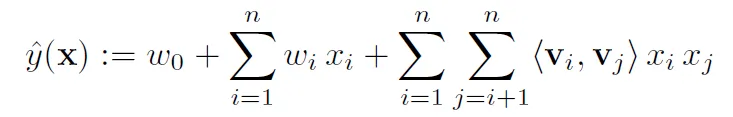
2維的FM公式

  1. $w_0$​是bias
  2. $w_i​$是特徵$i$的一維權重
  3. $w_{i,j}$​是特徵$i$和特徵$j$的二次交叉權重
  • 隱向量長度$k$為hyperparameter
  • FM將權重矩陣分解為隱向量的內積，破壞了權重的獨立性，所以在稀疏資料中仍能學習
    1. 已知一正定矩陣$W$，必存在$V$使$W=VV^t$
    2. 權重矩陣$W$必為正定
    3. 所以$W$必能分解成隱向量矩陣$V$乘自身的轉置
  • 原本$W$的大小為$\frac{n^2}{2}$，改成隱向量$V$之後大小為$kn$，$k$通常不會設很大，明顯減少參數數量
    • 限制$k$的大小也能限制FM模型的表達力，泛化能力較好

結構

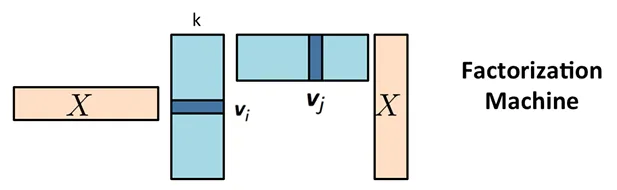
效率

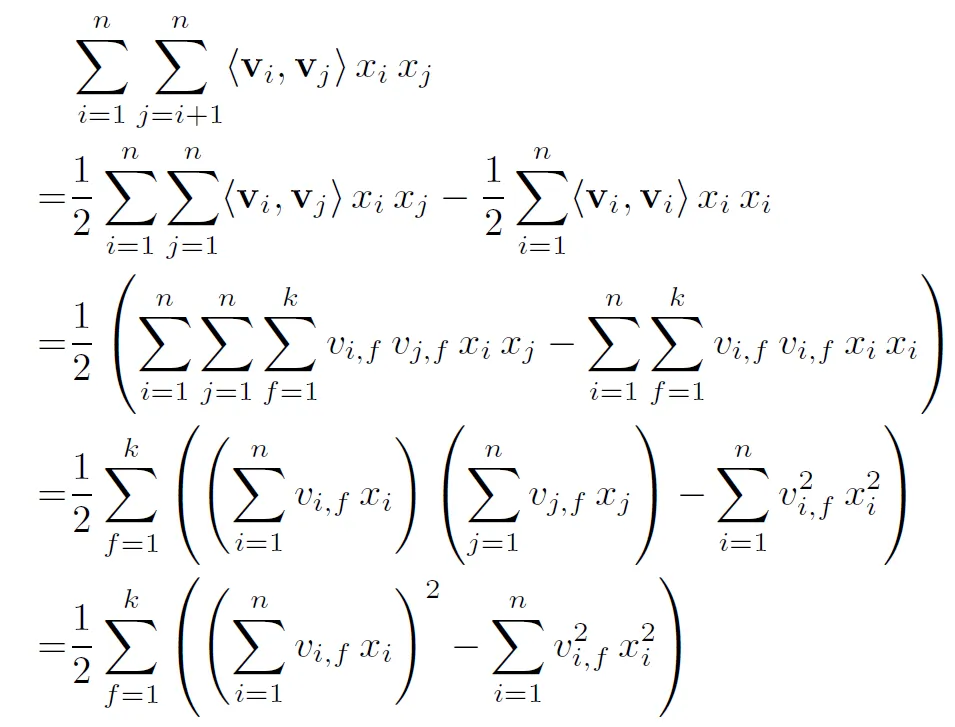
整理公式後，Inference的時間複雜度從$O(kn^2)$降到了$O(kn)$，$n$為特徵維度

  • 第2行公式推導：表示為整個矩陣扣掉對角項再除以2，因為$W$是對稱矩陣
  • 詳細推導可看這篇
  • 實作上只須計算非0元素的乘積，時間複雜度再下降到$O(km)$，$m$為平均一筆輸入資料中，值非0的特徵數

更新

使用gradient descent學習參數

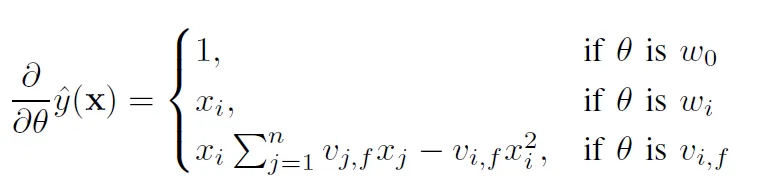
$\sum^n_{j=1}v_{j, f}x_j$可以事先計算，所以每次梯度更新的時間複雜度為$O(1)$

因此FM的訓練時間複雜度也是$O(km)$

高維度FM

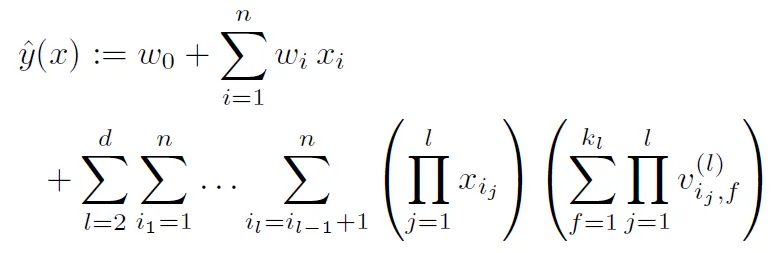
經過公式簡化(和二維的方法相似)，也可以在線性時間內計算

FM 和 Factorization Model, SVM 比較

論文中證明了兩件事

  1. 各種Factorization Model為FM的特化
  2. FM可以解決SVM在稀疏資料中無法成功訓練的問題

詳細證明看不懂，略過

結論

  • FM速度快、容易實作，於2012~14年為業界主流模型
  • FM產生的隱向量可視為一種embedding
    • 所以拿user的隱向量找相似隱向量的item，就是一個簡易且快速的推薦方法
  • FM適合類型特徵(離散)而非數值特徵(連續)，因為
    • 類型特徵可有多個隱向量，而數值特徵只有一個
    • 數值特徵不應使用同一個隱向量，如10歲和40歲
    • FM速度和非零特徵數有關，數值特徵類型化後不影響訓練速度

Field-aware factorization machines(FFM)

  • FM：一個特徵有一個隱向量
  • FFM：一個特徵有一組隱向量
    • 每個隱向量對應不同的特徵域
    • 特徵域通常為一群代表相同性質的特徵，如one-hot特徵

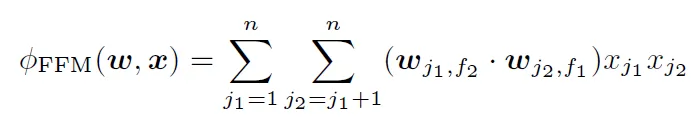
範例

  • 出版商特徵域(P): ESPN, Vogue, and NBC
  • 廣告商特徵域(A): Nike, Gucci, and Adidas
  • 消費者性別特徵域(G): Male, Female

在(ESPN, Nike) 和 (ESPN, Male) 中，ESPN的隱向量是不同的($V_{ESPN, A}$和 $V_{ESPN, G}$)

FM的隱向量：$$V_{ESPN}V_{Nike}, V_{ESPN}V_{Male}, V_{Nike}V_{Male}$$
FFM的隱向量：$$V_{ESPN, A}V_{Nike, P}, V_{ESPN, G}V_{Male,P}, V_{Nike, G}V_{Male,A}$$

結論

  • 訓練時間複雜度為$O(kn^2)$
  • 因為FFM的隱向量限制在一個特徵域，FFM的$k$可以比FM的$k$小

公式比較

只比較二次交叉項

$$FM(v, x) = ... + \sum^n_{j_1=1}{\sum^n_{j_2=j_1+1}{\langle v_{j_1}, v_{j_2}\rangle x_{j_1}x_{j_2}}}$$
$$FFM(v, x) = ... + \sum^n_{j_1=1}{\sum^n_{j_2=j_1+1}{\langle v_{j_1, f_2}, v_{j_2, f_1}\rangle x_{j_1}x_{j_2}}}$$

方法比較

  • FM：在LR(Logistic Regression)的基礎上，加入特徵交叉
  • FFM：在FM的基礎上，加入特徵域交叉

總結

就算Deep Learning盛行，FM也是一個很好的Baseline Model

Reference

  • Rendle, Steffen. "Factorization machines." 2010 IEEE International conference on data mining. IEEE, 2010
  • Juan, Yuchin, et al. "Field-aware factorization machines for CTR prediction." Proceedings of the 10th ACM conference on recommender systems. 2016
  • FM：推薦算法中的瑞士軍刀
  • Field-aware Factorization Machines with xLearn
  • http://web.cs.ucla.edu/~chohsieh/teaching/CS260_Winter2019/lecture13.pdf
  • 推薦系統系列（一）：FM理論與實踐
  • 初探Factorization Machine
  • 推薦系統算法FM、FFM使用時，連續性特徵，是直接作為輸入，還是經過離散化後one-hot處理呢？
  • FM模型連續特徵離散化